EQUAÇÕES DE GRACELI

VARIÁVEIS QUÂNTICAS E RELATIVISTAS DIMENSIONAIS DE INTERAÇÕES $\psi ^{*}$ $\psi$ ω $/ T / c} =$ EM:

G* = $\psi ^{*}$ = OPERADOR QUÂNTICO DE GRACELI.

EQUAÇÃO DE GRACELI.. PARA INTERAÇÕES DE ONDAS E INTERAÇÕES DAS FORÇAS FUNDAMENTAIS.

$\psi ^{*}$ [ $\psi ^{*}$ ${\boldsymbol {\mu }}$ ] $\lambda$ ω ${\mathcal {T}}$ , $\sigma$ , $\psi$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ [x,t] ] =

$\psi ^{*}$ $\psi$ ω $/ T / c} =$

$\psi ^{*}$ Em mecânica quântica, o OPERADOR DE GRACELI [ $G* =$ $\psi ^{*}$

$COMO TAMBÉM ESTÁ RELACIONADO A TODO SISTEMA CATEGORIAL GRACELI, TENSORIAL GRACELI DIMENSIONAL DE GRACELI..$

A distribuição de Wigner de uma função f(t) é uma função complexa W(ω,τ) dada pela expressão

{\mathcal {W}}\{f(t)\}\;=\;W(\omega ,\tau )\;=\;\int _{-\infty }^{\infty }f\left(\tau +{\frac {t}{2}}\right)\cdot f^{*}\left(\tau -{\frac {t}{2}}\right)\cdot e^{-i\omega t}\;dt\qquad (1a)

$\psi ^{*}$

\psi

ω $/ T] c} =$

f(t)\;=\;{\mathcal {W}}^{-1}\{W(\omega ,\tau )\}\;=\;{\frac {1}{2\pi \cdot f^{*}(0)}}\int _{-\infty }^{\infty }W\left(\omega ,{\frac {\tau }{2}}\right)\cdot e^{i\omega \tau }\;d\omega \qquad (1b)

Onduleta (português europeu) ou ondaleta (português brasileiro)[nota 1] (em inglês: wavelet) é uma função capaz de decompor e descrever ou representar outra função (ou uma série de dados) originalmente descrita no domínio do tempo (ou outra ou outras várias variáveis independentes, como o espaço), de forma a podermos analisar esta outra função em diferentes escalas de frequência e de tempo. A decomposição de uma função com o uso de wavelets é conhecida como "transformada wavelet" e tem suas variantes contínua e discreta. Graças à capacidade de decompor as funções tanto no domínio da frequência quanto no domínio do tempo, as funções wavelet são ferramentas poderosas de processamento de sinais, muito aplicadas na compressão de dados, eliminação de ruído, separação de componentes no sinal, identificação de singularidades, detecção de auto-semelhança, e muito mais.

A exemplo de outras transformadas, sua definição pode ser expandida de forma a abarcar um maior número de dimensões; por exemplo, para tratamento de imagens, pode-se usar a transformada de wavelet bidimensional.

De Fourier até wavelets

Na análise de Fourier podemos extrair apenas informações sobre o domínio da frequência, mas não podemos saber "quando" no tempo acontecem essas frequências que estudamos; enquanto isso, na análise com wavelets podemos extrair também informações da função no domínio do tempo. A resolução ou detalhamento da análise no domínio da frequência diminui enquanto a resolução no tempo aumenta, sendo impossível aumentar o detalhamento em um dos domínios sem diminuí-lo no outro (em uma analogia ao Princípio da incerteza de Heisenberg, chama-se esta relação entre os domínios da frequência e do tempo de relação de incerteza ou simplesmente de princípio da incerteza). Usando a análise de wavelets, é possível escolher a melhor combinação dos detalhamentos para um objetivo estabelecido.

Características

Para ser considerada uma wavelet, uma função tem de atender as seguintes características:

A área total sob a curva da função é 0, ou seja $\int_{-\infty}^{\infty} \psi (t) dt = 0 \qquad (1a)$
A energia da função é finita, ou seja $\int _{-\infty }^{\infty }|\psi (t)|^{2}dt\;\;\;<L\qquad L\in \mathbb {N} \qquad (1b)$ $\psi ^{*}$ $\psi$ ω $/ T] c} =$

Uma wavelet tipo chapéu mexicano.

Estas condições são equivalentes a dizer que $\psi(t)$ é quadrado integrável ou que pertence ao conjunto $\mathcal{L}^2(\R)$ das funções quadrado integráveis. As propriedades acima sugerem que $\psi(t)$ tende a oscilar acima e abaixo do eixo $t$ , e que tem sua energia localizada em uma certa região, já que ela é finita (condição de regularidade).

Essa característica de energia concentrada em uma região finita é que diferencia a análise usando wavelets da análise de Fourier, já que esta última usa as funções de seno e cosseno que são periódicas e infinitas. Uma outra forma de expressar a característica de regularidade é dizer que a transformação de wavelet é um operador local no domínio do tempo.

Para ser utilizada na análise de sinais uma função wavelet precisa também de outra característica que chamamos de condição de admissibilidade, e que permite a existência da "transformada inversa de wavelet". Esta característica será discutida mais abaixo.

Uma wavelet de Morlet.

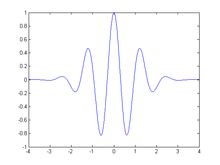
Alguns exemplos de funções que atendem estas características são a função wavelet de Morlet (ver figura ao lado):

$\psi(t)=e^{-t^2}cos \left ( \pi t \sqrt{\frac{2}{\ln{2}}} \right ) \approx e^{-t^2} \cos{(2.885 \pi t)} \qquad (2a)$ $\psi ^{*}$ $\psi$ ω $/ T] c} =$

e a curva conhecida como chapéu mexicano (em inglês: mexican hat), definida por:

$\psi(t) = (1 - 2t^2)e^{-t^2} \qquad (2b)$ $\psi ^{*}$ $\psi$ ω $/ T] c} =$

que é a segunda derivada da função Gaussiana $-0.5e^{-t^2}$

Transformada de wavelet contínua

A transformada de wavelet decompõe uma função definida no domínio do tempo em outra função, definida no domínio do tempo e no domínio da frequência. Ela é definida como:

$W(a,b) = \int_{-\infty}^{\infty} f(t) \frac{1}{\sqrt{|a|}}\psi^* \left ( \frac{t-b}{a} \right ) dt. \qquad (3a)$ $\psi ^{*}$ $\psi$ ω $/ T] c} =$

que é uma função de dois parâmetros reais, a e b. o símbolo * indica o conjugado complexo. Se definirmos $\psi_{a,b}(t)$ como:

$\psi_{a,b}(t) = \frac{1}{\sqrt{|a|}}\psi^* \left ( \frac{t-b}{a} \right ), \qquad (3b)$ $\psi ^{*}$ $\psi$ ω $/ T] c} =$

Podemos reescrever a transformada como o produto interno das funções $f(t)$ e $\psi_{a,b}(t)$ :

$W(a,b)=\left\langle f(t),\psi _{a,b}(t)\right\rangle =\int _{-\infty }^{\infty }f(t)\psi _{a,b}^{*}(t)dt.\qquad (3c)$ $\psi ^{*}$ $\psi$ ω $/ T] c} =$

A função $\psi(t)$ que equivale a $\psi_{1,0}(t)$ é chamada de "wavelet mãe" (em inglês: mother wavelet) enquanto as outras funções $\psi_{a,b}(t)$ são chamadas de "wavelets filhas". Estas têm a mesma forma geral que a wavelet mãe.

O parâmetro b indica que a função $\psi(t)$ foi transladada no eixo t de uma distância equivalente a b, sendo então um parâmetro de translação. Já o parâmetro a causa uma mudança de escala, aumentando (se $a > 1$ ) ou diminuindo (se $a<1$ ) a wavelet formada pela função. Por isto o parâmetro a é conhecido como parâmetro de escala (em inglês: scaling parameter). As wavelets filhas constituem, por conseguinte, uma família de curvas com forma idêntica à da wavelet mãe, deslocadas no tempo e escaladas em amplitude. No domínio do tempo, a transformada de wavelet é uma medida da correlação entre o sinal f(t) e as wavelets filhas.

O termo $\frac{1}{\sqrt{|a|}}$ é um fator de normalização que garante que a energia de $\psi_{a,b}(t)$ seja independente de a e de b, tal que:

$\int_{-\infty}^{\infty} |\psi_{a,b} (t)|^2 dt = \int_{-\infty}^{\infty} |\psi (t)|^2 dt \qquad (3d)$ [nota 2] $\psi ^{*}$ $\psi$ ω $/ T] c} =$

Há um vasto número de diferentes wavelets, cada adequada para diferentes aplicações.

Wavelets discretas

Coiflets

Cohen-Daubechies-Feauveau wavelet
Daubechies wavelet
Haar wavelet
Mathieu wavelet
Legendre wavelet
Villasenor wavelet
Symlets

Wavelets contínuas

Reais

Beta wavelet
Hermitian wavelet
Hermitian hat wavelet
Mexican hat wavelet
Meyer wavelet
Shannon wavelet
Gaussian wavelet
Cos-gaussian wavelet
Gabor wavelet

Complexas

Complex Mexican hat wavelet
Morlet wavelet
Shannon wavelet

Transformada inversa de wavelet

Como usamos wavelets para transformar uma função, precisamos também da transformada inversa, de forma a recompor o sinal no domínio do tempo a partir da sua decomposição. Se chamarmos de $\Psi(\omega)$ a transformada de Fourier da função $\psi(t)$ :

$\Psi (\omega )=\int _{-\infty }^{\infty }\psi (t)e^{-i\omega t}dt={\sqrt {a}}\cdot \Psi (a\omega )\cdot e^{-i\omega t}\qquad \omega ={\frac {2\pi }{a}}\qquad (4a)$ $\psi ^{*}$ $\psi$ ω $/ T] c} =$

e se $W(a,b)$ for a transformada de wavelet da função $f(t)$ usando a wavelet $\psi(t)$ , então temos que a transformada inversa é dada por:

$f(t) = \frac{1}{C} \iint\limits_{-\infty -\infty}^{\ \ \ \infty\ \infty} \frac{1}{|a|^2}W(a,b)\psi_{a,b}(t)da \ db, \qquad (4b)$ $\psi ^{*}$ $\psi$ ω $/ T] c} =$

onde $C=\int _{-\infty }^{\infty }{\frac {|\Psi (\omega )|^{2}}{|\omega |}}dw.\qquad (4c)$ $\psi ^{*}$ $\psi$ ω $/ T] c} =$

Este parâmetro $C$ necessita ser finito e positivo, o que nos leva a uma nova restrição. Esta restrição sobre o valor de $C$ é a condição de admissibilidade citada anteriormente.[nota 3]

Transformada de wavelet discreta

Ver artigo principal: Transformada discreta de wavelet

É derivada da transformada contínua fazendo-se a e b variáveis discretas, em lugar de contínuas, através de uma amostragem. O usual é tomar

$a\;=\;N^{j}\qquad b\;=\;kMa\qquad j,k\in \mathbb {N}$ $\psi ^{*}$ $\psi$ ω $/ T] c} =$

A wavelet mãe resultante é uma grade (matriz) de valores h[j,k] relacionada à wavelet contínua ψ(t) pela expressão

$h[j,k]\;=\;N^{\frac {-j}{2}}\cdot \psi \left({\frac {t}{N^{j}}}-kM\right)$ $\psi ^{*}$ $\psi$ ω $/ T] c} =$

Quanto mais próximo de 1 o valor de N, mais a versão discreta se aproxima da versão contínua. N normalmente é feito igual a 2 e M igual a 1, para agilizar os cálculos em computadores e obter-se um número de coeficientes hi,j não muito grande, e ainda conservando toda a informação original de f(t).

De forma similar, a transformada discreta é uma matriz de coeficientes Wj,k dados por

$W[j,k]\;=\;\sum _{k=1}^{m}\sum _{j=1}^{n}f[k]\cdot h^{*}[j,k]\;=\;\langle f,h\rangle \qquad (3e)$ $\psi ^{*}$ $\psi$ ω $/ T] c} =$

onde o asterisco denota o conjugado complexo e f[k] é a sequência de amostras obtida de f(t). A distância entre os pontos da grade W não é uniforme, refletindo a propriedade de auto-escalamento da transformada de wavelet contínua. Os limites n e m são determinados indiretamente pela escolha de N e M.

A transformação inversa é uma operação mais delicada, uma vez que a amostragem pode levar a perda de informação. Por isso, não se pode simplesmente aplicar a fórmula da inversão, que é uma versão discreta das fórmulas (4b) e (4c)

$f(t)\cong f[k]\;=\;\sum _{k=1}^{m}\sum _{j=1}^{n}W[j,k]\cdot h[j,k]\;=\;\langle W,h^{*}\rangle \qquad (4d)$ $\psi ^{*}$ $\psi$ ω $/ T] c} =$

sem verificar se os coeficientes W foram calculados adequadamente. Por esse motivo, existe outra técnica para a inversão, baseada na análise do sinal em múltiplos níveis de resolução por meio de codificação de sub-bandas (em inglês: subband coding): a teoria das "wavelets ortonormais", desenvolvida por Mallat e Meyer em 1986.

Em aplicações práticas, como é muito difícil obter uma expressão analítica para a transformada contínua, é a versão discreta, calculada por computador, que é empregada. Um dos motivos da popularidade da transformada de wavelet discreta é a existência de um algoritmo que permite calcular os coeficientes com esforço de ordem O(L), onde L é o tamanho dos dados origiais (ou seja, das amostras de f(t) e de ψ(t)). Esse algoritmo é chamado de "transformada rápida de wavelet" (em inglês: FWT, Fast Wavelet Transform). Deve-se salientar que ele é ainda mais eficiente do que o muito conhecido algoritmo da transformada rápida de Fourier (FFT).

Subband coding

Seja uma função p(t) a resposta de um filtro passa-baixa. A partir dela pode-se gerar uma família de funções pj,k tais que

$p_{j,k}(t)\;=\;2^{\frac {-j}{2}}\cdot p\left({\frac {t}{2^{j}}}-k\right)\qquad (3e)$ $\psi ^{*}$ $\psi$ ω $/ T] c} =$

Se essas funções forem aplicadas ao sinal a ser analisado f(t) por meio de uma operação de correlação análoga a (3c)

$g_{j,k}(t)=\int _{-\infty }^{\infty }f(t)\cdot p_{j,k}^{*}(t)\;dt\qquad (3f)$ $\psi ^{*}$ $\psi$ ω $/ T] c} =$

isso "alisará" o sinal, resultando numa aproximação gj,k(t) para aquela escala definida pelos parâmetros j e k. Cada filtragem equivale a uma sub-amostragem (downsampling) adicional por um fator igual a 2. A perda de detalhe em cada filtragem é dada pela diferença entre duas funções g consecutivas:

$d_{j,k}(t)=g_{j,k}(t)\;-\;g_{j,k-1}(t)\qquad (3g)$ $\psi ^{*}$ $\psi$ ω $/ T] c} =$

O sinal original pode ser perfeitamente reconstruído a partir da soma das funções dj,k(t). Assim, a representação por meio das funções dj,k(t) não leva a perda de informação e ainda constitui uma representação mais compacta de f(t). Matematicamente, o que ocorre é que a autocorrelação do sinal, que é dada exatamente pelo conjunto das funções gj,k(t), constitui uma redundância, que foi eliminada no processo.

A funções dj,k(t) podem ser computadas de outra forma: por meio de uma filtragem obtida pela correlação do sinal filtrado com uma função q(t) que é a resposta de um filtro passa-alta

$d_{j,k}(t)=\int _{-\infty }^{\infty }g_{j,k-1}(t)\cdot q_{j,k}^{*}(t)\;dt\qquad (3h)$ $\psi ^{*}$ $\psi$ ω $/ T] c} =$

A relação entre duas funções q sucessivas é a mesma dada por (3f).

O sinal original pode ser perfeitamente reconstruído a partir da soma das funções g1,1(t) e d1,1(t). Além disso, qualquer uma das aproximações gj,k(t) pode ser reconstruída a partir das funções g e d posteriores, referentes a k + 1.

A técnica de subband coding, na prática, não utiliza apenas um par de filtros como descrito acima, e sim um conjunto de filtros passa-faixa, para maior eficiência e precisão.

Wavelets ortonormais

Wavelets ortonormais são obtidas através da decomposição do sinal por meio de duas funções ψ e φ, a primeira sendo a wavelet mãe e a segunda, a "wavelet pai" ou "função de escalamento". A wavelet pai é uma função contínua e de quadrado integrável, mas não satisfaz a condição (1a); em geral, seu valor médio é normalizado em 1. Usualmente, os valores são reais. ψ e φ satisfazem a (3f).

As wavelets pai e mãe descrevem o banco de filtros passa-faixa a ser empregados na análise por meio de subband coding.

O cálculo das funções ψ e φ discretas comporta algumas sutilezas adicionais em relação às versões contínuas representadas nas fórmulas acima. Mais importante, as wavelets pai e mãe precisam atender à chamada "condição de reconstrução perfeita".

Propriedades

Conservação da energia

Após a transformação, a energia do sinal se conserva, pois vale a relação

$\iint \limits _{-\infty -\infty }^{\ \ \ \infty \ \infty }\left|{\frac {W(a,b)}{a}}\right|^{2}\;db\;da\;=\;C\int _{-\infty }^{\infty }\left|{\frac {}{}}f(t)\right|^{2}\;dt\qquad (5a)$ $\psi ^{*}$ $\psi$ ω $/ T] c} =$

que equivale ao teorema de Parseval para a transformada de Fourier.

Quase-ortogonalidade

Uma vez que as diversas wavelets possuem escalas diferentes e estão defasadas no tempo, elas não constituem uma base ortogonal. No entanto, como pode-se sempre reconstruir o sinal original a partir da transformada, diz-se que elas constituem uma "base quase-ortogonal"; essa base contém informação redundante, mas não se perde informação na transformação.

Localidade

Apesar de qualquer função quer atenda às equações (1a), (1b) e (4c) poder ser empregada como wavelet mãe, em aplicações práticas em geral se exige a condição adicional

$\int _{-\infty }^{\infty }t^{p}\cdot \psi (t)\;dt\;=\;0\qquad p\in \mathbb {N} ^{*}\qquad (5b)$ $\psi ^{*}$ $\psi$ ω $/ T] c} =$

Quanto maior o valor de p, mais localizada é a wavelet no tempo, e por conseguinte também W(a,b), que decai no mínimo tão rápido quanto ap+½ o que é bastante vantajoso. Isso implica a wavelet ser localizada no domínio da frequência também, não apenas no domínio do tempo. Essa propriedade é também conhecida como "regularidade da wavelet".

Transformada de Fourier da wavelet mãe

De acordo com as propriedades da transformada de Fourier, a condição (1a) implica

$\Psi (0)\;=\;0\qquad (5c)$

e a condição (5b) implica

$\left.{\frac {d^{n}}{d\omega ^{n}}}\Psi (\omega )\right|_{\omega =0}\;=\;0\qquad n\;\leq \;p\qquad (5d)$ $\psi ^{*}$ $\psi$ ω $/ T] c} =$

Isso significa que, quanto mais localizada no tempo for a wavelet mãe, mais achatado é o seu espectro em ω = 0.

Linearidade

${\mathcal {W}}\{cf(t)+dg(t)\}\;=\;c\cdot {\mathcal {W}}\{f(t)\}\;+\;d\cdot {\mathcal {W}}\{g(t)\}\qquad (5e)$ $\psi ^{*}$ $\psi$ ω $/ T] c} =$

Deslocamento no tempo

${\mathcal {W}}\{f(t+c)\}\;=\;W(a,b-c)\qquad (5f)$ $\psi ^{*}$ $\psi$ ω $/ T] c} =$

Escalamento no tempo

${\mathcal {W}}\{f(ct)\}\;=\;{\sqrt {\frac {1}{c}}}\cdot W(ac,bc)\qquad (5g)$ $\psi ^{*}$ $\psi$ ω $/ T] c} =$

Transformada de uma constante

${\mathcal {W}}\{k\}\;=\;0\qquad (5h)$ $\psi ^{*}$ $\psi$ ω $/ T] c} =$

Transformada de uma função linear

${\mathcal {W}}\{t\}\;=\;-i{\sqrt {a^{3}}}\cdot \left.{\frac {d}{d\omega }}\Psi ^{*}(\omega )\right|_{\omega =0}\qquad (5i)$ $\psi ^{*}$ $\psi$ ω $/ T] c} =$

onde i é a unidade imaginária e * indica o conjugado complexo. Em geral, devido a (5b), W(a,b) = 0 neste caso.

Análise

A análise de wavelet é feita pela aplicação sucessiva da transformada de wavelet com diversos valores para a e b, representando a decomposição do sinal original em diversos componentes localizados no tempo e na frequência, de acordo com estes parâmetros. Cada wavelet possui melhor ou pior localização nos domínios da frequência e do tempo, por isso a análise pode ser feita com wavelets diferentes de acordo com o resultado desejado.

A análise wavelet traz consigo uma análise em resoluções múltiplas, onde o nível de resolução é dado pelo índice $a$ . Nesta análise em resoluções múltiplas, geramos uma sequência de subespaços encaixantes, onde as funções de base numa escala $a_0$ não "enxergam" detalhes de tamanho menor que $2^{-a_0}$ .

Transformação como um filtro

A transformada de wavelet pode ser interpretada como o resultado da passagem do sinal por um banco de filtros passa-faixa de resolução variável. O fator de qualidade (ou fator Q) desses filtros é dado pela fórmula tradicional

$Q\;=\;{\frac {\omega _{c}}{\Delta \omega }}\qquad (6a)$ $\psi ^{*}$ $\psi$ ω $/ T] c} =$

onde ωc é a frequência central e Δω é a largura de banda de cada filtro, que por sua vez é dada por

$\Delta \omega \;=\;{\sqrt {\frac {\int _{-\infty }^{\infty }\omega ^{2}\cdot |G(\omega )|^{2}\;d\omega }{\int _{-\infty }^{\infty }|G(\omega )|^{2}\;d\omega }}}\qquad (6b)$ $\psi ^{*}$ $\psi$ ω $/ T] c} =$

onde G(ω) é a resposta em frequência do filtro. Para a transformada de wavelet,

$\omega _{c}(a)\;=\;{\frac {1}{a}}\;\omega _{c}(1)\qquad (6c)$ $\psi ^{*}$ $\psi$ ω $/ T] c} =$

$\Delta \omega (a)\;=\;{\sqrt {\frac {\int _{-\infty }^{\infty }\omega ^{2}\cdot |\Psi (a\omega )|^{2}\;d\omega }{\int _{-\infty }^{\infty }|\Psi (\omega )|^{2}\;d\omega }}}\;=\;{\sqrt {\frac {\int _{-\infty }^{\infty }(a\omega )^{2}\cdot |\Psi (a\omega )|^{2}\;d(a\omega )}{\int _{-\infty }^{\infty }a^{2}\cdot |\Psi (a\omega )|^{2}\;d(a\omega )}}}\;=\;{\frac {1}{a}}\;\Delta \omega (1)\qquad (6d)$

$\psi ^{*}$ $\psi$ ω $/ T] c} =$

ou seja, a frequência central e a largura de banda de cada filtro são inversamente proporcionais a a, o fator de escala. Com isso, o fator de qualidade Q é constante, o que proporciona uma análise com a mesma fidelidade em todas as escalas.